Superconductors.ORG herein reports finding a surprising similarity between the R-T plots of superconductors and the bode plots of active filters. Active filters are electronic devices used to attenuate or pass certain frequencies - aural, rf, or optical. For example a 1000 HZ high-pass audio filter only allows frequencies above 1000 HZ to pass. Frequencies below 1000 HZ are suppressed. Since superconductivity is facilitated by lattice vibrations (phonons) it stands to reason that the wave function of a superconductor should mirror the transfer function of an active filter. And this has now been confirmed in the plots on this page.
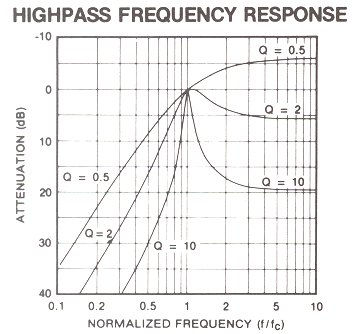
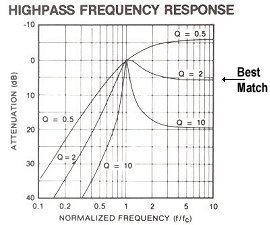
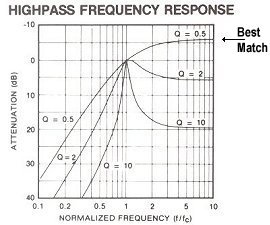
In the below two graphics a superconductor R-T plot is shown alongside three high-pass filter (HPF) plots with different "Q's". The slope of an HPF curve is determined by "Q" or "quality" factor. The higher the Q, the steeper the slope. Since this copper-oxide transitions to a superconductive state fairly quickly, its equivalent Q would be just over 2 (see "Best Match" arrow).
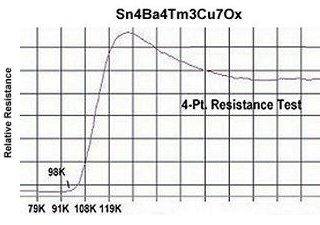
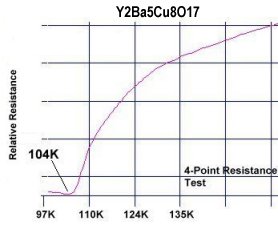
The below graphics illustrate a superconductor with a more gradual slope. On the left is Y-258, a superconductor that transitions over dozens of degrees of temperature change. Below right the active filter analog with a Q of 0.5 mirrors that slope most closely (see arrow).
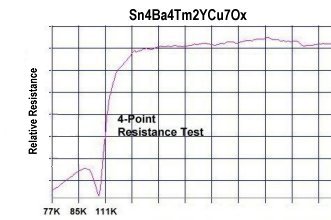
Novel superconductors like "reentrant" and "resonant" types can also be characterized using active filter plots. Below left is a reentrant high temperature superconductor with twin transitions. Its active filter analog is shown below right.
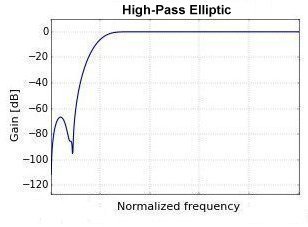
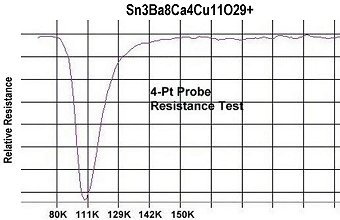
The below left graphic is from a resonant high temperature superconductor. Its active filter analog is a "notch" type, shown at right. Again the "Q" of the filter comes into play. Its best match would have a low Q.
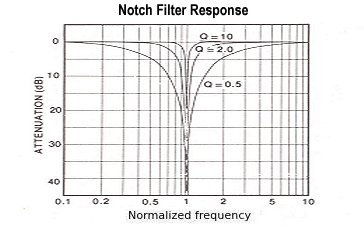
Of course, characterizing superconductors in this way then begs the question: Since all active filter circuits can be quantified with a formula, could this lead to a formula that finally explains high-temperature superconductivity? Stay tuned!
E. Joe Eck
© 2021 - 2024 Superconductors.ORG
All rights reserved.
BACK to "News" page at Superconductors.ORG